La méthode quantile-quantile consiste à élaborer une fonction de correction pour ramener la distribution statistique des données simulées à celle des valeurs observées, pour chaque variable, saison et période concomitante. Cette méthode non paramétrique revient à considérer que le modèle est capable de prédire la distribution des variables climatiques mais pas la valeur exacte de chaque quantile (Déqué et al., 2007).

Pour chaque variable météorologique, les fonctions de densité de probabilités (PDF) sont calculées en chaque point des séries temporelles de la simulation et des séries dites observées (climat de référence représenté par la base de données SAFRAN). La fonction de transfert consiste à associer chaque centile du modèle au centile observé. Pour le futur, on cherche à quels centiles correspond la valeur du jour de la projection, on associe les valeurs en climat présent, puis on effectue une interpolation linéaire entre les centiles. Au-delà du dernier centile estimé et en deçà du 1er, on applique une correction constante estimée sur le centile extrême correspondant. Dans certains cas (précipitations, humidité relative) on n’a pas d’extrapolation puisqu’il existe un extremum absolu d’un ou des deux côtés de la fonction (distribution bornée). Cette méthode permet de corriger les plus gros défauts des modèles notamment en termes d’intensité des phénomènes extrêmes ou de fréquence de jours pluvieux (fréquence surestimée lorsque le modèle est trop zonal).

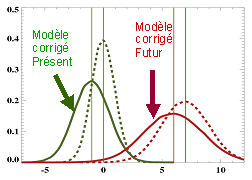
• Les grandes étapes de la méthode :

•  

L’idée est de corriger le spectre des variables météorologiques simulées en chaque point de grille, en ramenant les valeurs des quantiles du modèle à celles données par SAFRAN.

Concrètement, l’opération s’effectue en quatre étapes :

– Les variables météorologiques quotidiennes simulées sur la période sont interpolées sur la grille SAFRAN. L’interpolation consiste à prendre pour chaque point de la grille SAFRAN la valeur du quantile simulé au point le plus proche de la grille du modèle, ceci afin de ne pas lisser le champ par une opération de moyenne.

– On calcule les quantiles,  le plus souvent au pas de 1 % mais avec une résolution de 0,5 % ou même parfois 0,1 % pour les queues de distribution,  des variables météorologiques quotidiennes de la simulation considérée et de SAFRAN, en prenant en compte une période commune (climat de référence).

– En chaque point i de la grille SAFRAN et pour chaque ordre k de quantile, on calcule alors le coefficient de correction Corr(k) donné par la formule suivante :

Corrk(i) = 0 si Qk(i) = 0

Corrk(i) = QkSAF (i) / Qk(i) si Qk(i) ≠ 0

Où Qk(i) est la valeur au point i du quantile modèle interpolé sur la grille SAFRAN d’ordre k et QkSAF (i) la valeur du quantile SAFRAN correspondant.

Ce coefficient de correction Corr(k) est utilisé plus loin pour un ajustement linéaire de la correction entre deux quantiles.

– Pour chaque jour j de la période et en chaque point i de la grille SAFRAN, on cherche l’ordre k du quantile modèle (interpolé) directement inférieur à la valeur de la variable (précipitation ou température) quotidienne du jour j au point i (RR(j,i)) :

k=0,999 si RR(j,i) ≥ Q0,999(i) sinon, k est tel que : Qk(i) ≤ RR(j,i) ≤ Qk+1(i)

RRcorr(j,i), la variable (précipitation ou température) corrigée du jour j au point i, est alors donnée par la formule suivante : Rrcorr(j,i)=RR(j,i)Corrk(i)

• Remarques :

•  

– La méthode repose sur une hypothèse forte selon laquelle la fonction de transfert calibrée sur une période du passé reste valable dans le futur (hypothèse de stationnarité qui n’est pas démontrable).

– On fait aussi l’hypothèse que le modèle ne simule pas une variable physique mais un rang dans sa propre échelle de valeurs.

– Tous les traitements sont faits point de grille par point de grille.

– Chaque variable est corrigée indépendamment. L’interdépendance entre variables n’est donc pas préservée.

– C’est une méthode qui est adaptée pour l’étude des extrêmes, pour évaluer les fréquences de dépassements de seuils en certains points, car la correction à apporter à la valeur simulée tient compte de sa fréquence d’occurrence (événement plus ou moins rare).

– En outre cette technique a l’avantage de présenter une bonne cohérence temporelle permettant, par exemple, l’étude de périodes de sécheresse ou de nombre de jours consécutifs de fortes précipitations ou de fortes/faibles températures. Toutefois, elle ne permet pas de corriger les défauts que peuvent présenter les simulations en termes de variabilité aux pas de temps longs (variabilité inter-annuelle par exemple).

– Il existe un effet de seuils en fonction du nombre de quantiles utilisés qui peut entraîner une mauvaise reconstitution des extrêmes. Dans le cas où le modèle simulerait dans la période à corriger de valeurs extrêmes supérieurs aux derniers quantiles de la période d’apprentissage, Déqué et al., 2007 propose d’extrapoler la correspondance établie sur la période d’apprentissage, selon une pente constante qui tend vers 1 et qui présente à la fois des avantages et des inconvénients.

• Références :

•  

Déqué M. et al., 2007 : Frequency of precipitation and temperature extremes over France in an anthropogenic scenario : model results and statistical correction according to observed values. Global and Planetary Change. 57 : 16-26.